Standard Deviation

In statistics and probability theory, standard deviation (represented by the symbol sigma, σ) shows how much variation or “dispersion” exists from the average (mean, or expected value). A low standard deviation indicates that the data points tend to be very close to the mean; high standard deviation indicates that the data points are spread out over a large range of values.

Source: Wikipedia

Steps to calculate the Standard Deviation:

1. Find the mean of the sample population
2. Compute the difference of each data points from mean and then square the difference.
3. Compute the average of these values, and then take a square root.

Kdb provides dev function to calculate the standard deviation. However, it is a bit different from STDEV function of excel.

Check out my earlier post Difference between standard deviation function of MS Excel and KDB

Effect of outliers in Standard Deviation :

An outlier is a datum that is too large or too small in value as compared to the other data. Since mean is most affected by outliers, as same weight is given to all the data points, so is Standard Deviation.

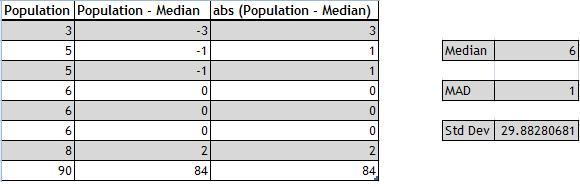
Let’s consider the same population which we have used in the above example to calculate Standard Deviation with an outlier (90). The impact of the outlier is drastic which can be seen in the following example.

Always remember that these points remain observations and you should not just throw them out. Instead, you should have good reasons to remove your outliers.

In data analysis, sometimes Median Absolute Deviation(MAD) is used instead of Standard Deviation.

Check out my another post on Median Absolute Deviation for more details and how to calculate it in KDB.

Median Absolute Deviation

In statistics, the median absolute deviation (MAD) is a robust measure of the variability of a univariate sample of quantitative data. It can also refer to the population parameter that is estimated by the MAD calculated from a sample.

For a univariate data set X₁, X₂, …, X_n, the MAD is defined as the median of the absolute deviations from the data’s median:

that is, starting with the residuals (deviations) from the data’s median, the MAD is the median of their absolute values.

Source: Wikipedia

As described in my previous post  Standard Deviation, MAD is mostly used to overcome the outlier effect on sample population. It is a robust statistic, being more resilient to outliers in a data set than the standard deviation. In the standard deviation, the distances from the mean are squared, so large deviations are weighted more heavily, and thus outliers can heavily influence it. In the MAD, the deviations of a small number of outliers are irrelevant.

Example:

q Solution

q)d:3 5 5 6 6 6 8 90

q)mad:{med abs d-med[x] }

q)mad d
1f

q)stdevExcel:{c:count x; (dev x)*sqrt c%c-1 }

q)stdevExcel d
29.88281

q)dev d
27.95281

Absolute deviation

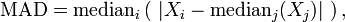
In statistics, the absolute deviation of an element of a data set is the absolute difference between that element and a given point. Typically the deviation is reckoned from the central value, being construed as some type of average, most often the median or sometimes the mean of the data set.

where

D_i is the absolute deviation,

x_i is the data element

and m(X) is the chosen measure of central tendency of the data set—sometimes the mean (), but most often the median.

Source : Wikipedia

Average absolute deviation

The average absolute deviation of a data set is the average of the absolute deviations. Note here we are talking about averaging the absolute deviation calculated using the mean, median, mode, or some another measure of central tendency.

The average absolute deviation of a set {x₁, x₂, …, x_n} is

The choice of measure of central tendency, , has a marked effect on the value of the average deviation. For example, for the data set {2, 2, 3, 4, 14}:

Measure of central tendency	Average absolute deviation	Method
Mean = 5		Mean Absolute Deviation using Mean
Median = 3		Mean Absolute Deviation using Median
Mode = 2		Mean Absolute Deviation using Mode

There are several other Absolute Deviation method exist like Median Absolute Deviation using Median, Maximum Absolute Deviation using Mean etc which are simply combination of various Central Tendencies and the aggregation of Absolute Deviation.

q functions

For calculating the aforementioned Central Tendencies , q already provides functions to calculate the median(med) and mean(avg). There is no function to calculate the mode, however implementation is pretty much straightforward. Checkout my another post Mode where i have already implemented mode in q.

q)med 2 2 3 4 14
3f

q)avg 2 2 3 4 14
5f

k)mode:{&:max[c]=c:#:'=:x}

q)mode 2 2 3 4 14
enlist 2